Рассмотрим простую задачу по поиску максимально длинной сбалансированной подстроки. Задача предоставлена сайтом codeforces.com. Использовать будем язык Java. Вот условие:
Задана строка s, состоящая только из символов 0 и 1. Подстрока [l, r] в s — это строка slsl + 1sl + 2… sr, ее длина равна r - l + 1. Подстрока называется сбалансированной, если количество нулей (0) в ней совпадает с количеством единиц.
Найдите длину наидлиннейшей сбалансированной подстроки s.
В первой строке записано одно целое число n (1 ≤ n ≤ 100000) — длина строки s.
Вторая строка — строка s длиной ровно n. В s содержатся только символы 0 и 1.
Если в s нет ни одной непустой сбалансированной подстроки, то выведите 0. Иначе выведите длину наидлиннейшей сбалансированной подстроки.
|
1 2 |
8 11010111 |
|
1 |
4 |
|
1 2 |
3 111 |
|
1 |
В первом примере можно выбрать подстроку [3, 6]. Она сбалансирована, длина — 4. Также можно выбрать подстроку [2, 5].
Во втором примере нет ни одной непустой сбалансированной подстроки.
Из условия задачи заключаем, что нам необходимо найти подстроку максимальной длины, в которой количество 0 и 1 будет одинаковым. Как нам это сделать? Мы будем последовательно сравнивать каждый символ строки на равенство 0 или 1 и записывать их количество. В момент, когда оно будет равным, необходимо записать длину текущей сбалансированной подстроки. Эти действия будем проводить, пока не достигнем конца строки. В момент когда это произойдет, отбросим первый элемент строки, и будем проводить те же операции подсчета количества 0 и 1 в оставшейся строке, размером – 1. После сдвигаем границу еще на шаг вперед и так далее, пока строка для сравнения не сократиться до размера одного последнего символа.
Приведу пример. Рассмотрим последовательность [ 0 1 1 0 1 ].
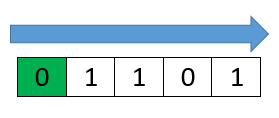
На первом проходе мы начинаем считать количество 0 и 1 с первого элемента. Первый элемент 0, добавили 1 к количеству нулей, второй 1 – добавили 1 к единицам. Сравниваем равенство количеств, они равны. Сохраняем в отдельную переменную длину сбалансированной подстроки. Она равна 2. Продолжаем идти по массиву. Достигнув 4 элемента у нас по 2 нуля и 2 единицы. Это тоже сбалансированная подстрока, сохраняем ее в переменную. Достигнув конца строки, отбрасываем первый элемент и делаем второй проход.

Начиная со второго элемента, так же считаем количество 0 и 1. И так далее
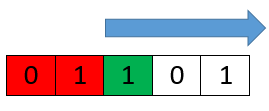
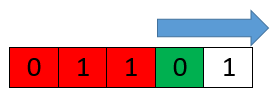
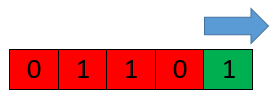
Сдвинув границу максимально вправо мы заканчиваем выполнения обходов. Мы проверили абсолютно каждую подстроку, и проверили их на сбалансированность. Осталось выбрать максимальный элемент из сохраненных длин сбалансированных строк.
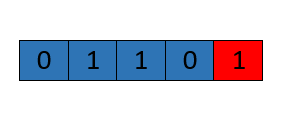
Длина максимальной подстроки равна 4. (выделена синим цветом).
Сложность алгоритма
Мы выполняем всего N шагов и в каждом делаем по N-i обходов. Получается что сложность равна O(N^2). Очень далеко от идеала. Предложенный алгоритм является наивным и, как мне кажется, самым простым решением “в лоб”. Исходный код задачи, так же далек от идеала. Поэтому предлагаю вам в комментариях предложить свои варианты алгоритмов, улучшить мой исходный код алгоритма, а так же написать реализацию предложенного вами алгоритма на языке Java и так же оставить его в комментариях.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
import java.util.*; public class Solution { public static void main(String[] args) { Scanner scan = new Scanner(System.in); int n = scan.nextInt(); // считываем длину строки String s = scan.next(); // считываем саму строку char[] c = s.toCharArray(); // преобразуем ее в массив символов int countOne = 0; // иницилизируем счетсчки int countZero = 0; int startBorder = 0; // заводим начальную границу int nextStartBorder = 1; // и следующую за ней List<Integer> lengthSubstrs = new ArrayList<>(); // хранить длины подстрок будем списков while (nextStartBorder < n) { // пока не достигли конца строки if (Objects.equals(c[startBorder], '0')) // проверяем чему равен элемент countZero++; // и увеличиваем его счетчик else countOne++; if (countOne == countZero) lengthSubstrs.add((startBorder + 1) - (nextStartBorder - 1)); startBorder++; // в случае равенства сохраняем длину и переходим к следующему элементу if (startBorder == n) { // если достигли конца строки, то startBorder = nextStartBorder; // переходим к следующей границе nextStartBorder++; // увеличиваем так же новую следующую границу countZero = 0; // обнуляем счетчики countOne = 0; } } if (lengthSubstrs.isEmpty()) // если список пуст, значит в строке нет сбалансированных System.out.println(0); // подстрок - выводи 0 else // иначе выводим максимальную длину System.out.println(Collections.max(lengthSubstrs)); } } |





3 comments On Разбор задачи “Сбалансированная подстрока”
Николай, спасибо большое за предоставленые решения!
У меня только один вопрос – а вы задачи отправляете на codeforces, чтобы убедиться, что Ваше решение полное?
Конечно! Все решения проходят тесты на codeforces. Предоставленное решение умышленно не пройдёт один из тестов на codeforces, потому что ограничение по времени в 1 секунду не будет выполнено из-за высокой сложности алгоритма. Предлагаю вам подумать над задачей и предложить реализацию более эффективного алгоритма)
Какая талантливая мысль